大模型训练-优化器整理

优化器指的是对于我们的一堆模型参数 θ ，以及一个损失函数 L(θ) ，如何找到找到 L(θ) 的最小值。

SGD

随机梯度下降 Stochastic Gradient Descent SGD 是最为基础的梯度下降方法。

其核心思路是：在每一步迭代中，用当前的梯度，按着负梯度方向把参数“推”一点，直到 loss 变得更小。

对于一个模型参数 θ，目标是最小化损失函数 L(θ)，SGD 每一步的更新公式是：

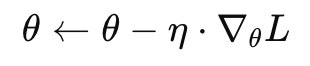
• θ：模型参数

• η：学习率（step size）

• ∇θL：当前梯度

依据更新时使用的样本数的不同，它可以分为多种类型：

• 如果用 整个训练集 来计算一次梯度，叫 Batch Gradient Descent

• 如果用 一个样本 来计算梯度，叫 True SGD

• 如果用 一个小批量样本（如32、64、128），叫 Mini-batch SGD（最常用）

Mini-batch SGD 就是现在主流训练方法——又能并行训练，又比逐样本快。

SGD足够简单和直观，但是SGD也有一些明显的缺点：

Momentum

Momentum（动量法） 是在 SGD 基础上的进行了优化，它引入了动量机制，它用过去的“梯度方向”给当前的更新加“惯性”！像小球在山谷中滑行，会积蓄动能，不会被小坑困住。

Momentum的更新公式如下：

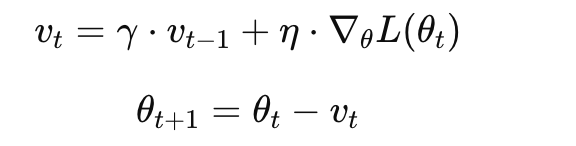
• γ：动量系数（一般取 0.9 或 0.99）

• v_t：累计的更新速度（类似速度向量）

• η：学习率

• ∇θL(θt)：当前梯度

v_t累积了过去的动量，使得在进行梯度更新的时候具有了惯性。

但是它也存在明显的缺点：

AdaGrad

SGD的一个问题在于所有参数都共用同一个学习率，而这会导致：

• 大梯度的参数震荡很厉害

• 小梯度的参数几乎不更新

为此AdaGrad提出依据历史的梯度信息来调整学习率。其参数更新的计算公式如下：

首先记录每个参数过去所有的梯度平方的“累计值”：

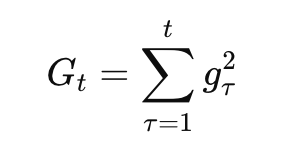
然后更新参数的时候，把学习率除以这个值的平方根：

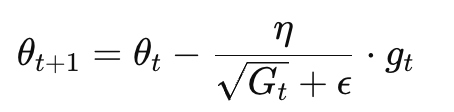
• θt：第 t 次迭代的参数

• η：初始学习率

• g_t：当前梯度

• G_t：当前参数的梯度平方和

• ϵ：防止除以 0 的小常数（如 1e−8）

在这种方法下就很好的解决了之前的问题：

• 如果某个参数的历史梯度一直很大，那它的 GtG_tGt 就大，学习率就变小 → 避免剧烈震荡

• 如果某个参数的历史梯度一直很小，学习率就不怎么缩 → 它还能继续学

但是它也存在一个明显的缺点，那就是因为G_t是不断累积的，所以到了后期梯度会变得很小，导致模型参数基本不更新。

RMSProp

为了解决AdaGrad随着时间推移，模型参数基本不更新的问题，RMSProp被提出。

它用指数加权移动平均（EMA）来更新梯度的平方，公式如下，即E[g^2]_t中越往前的梯度f对于当前的E[g^2]_t的影响就越小,从而使得学习率最后不会降为0，而是一直保持一定的平衡：

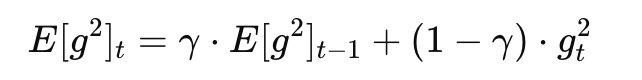
然后更新参数时使用：

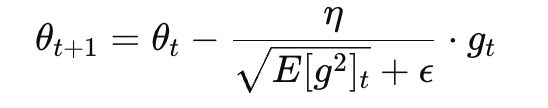
• γ：衰减系数（典型值 0.9）

• η：学习率

• g_t：当前梯度

• E[g^2]_t：当前参数历史梯度平方的加权平均

• ϵ：小常数，防止除以 0

类比理解一下：

• AdaGrad：你每次都把经验“记下来”，越记越多，最后太谨慎，啥都不敢动了 🙈

• RMSProp：你只记“最近几次”的经验 → 有记忆，但也保持灵活，适应当前环境 🧠✨

Adam

总的来说，Adam = Momentum + RMSProp + 偏差校正，它是一种带动量的、带自适应学习率的优化器。

它吸收了前人经验，既有方向记忆（动量），又能差异化学习率（RMSProp思想），而且还做了聪明的偏差修正，让前期更新不“失控”。

Adam 给每个参数记录了两个“动量”：

• 一阶矩（梯度的滑动平均）：

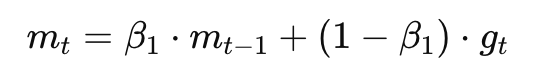
像 Momentum：记录梯度方向的平均值

• 二阶矩（梯度平方的滑动平均）：

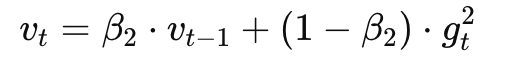
像 RMSProp：记录梯度的幅度变化（用于调整每个参数学习率）

此外由于在训练初期，m_t和v_t会偏向于 0（因为一开始动量积累值太小）

Adam 加了修正项：

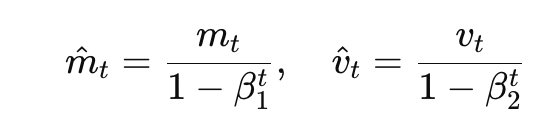
最终参数更新的公式如下：

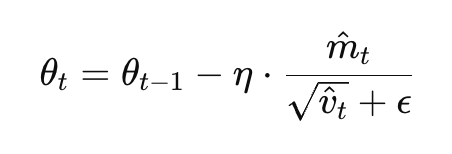
可视化理解一下的话，Adam 就像一个聪明的登山者：

• 手里有指南针（动量）🧭

• 脚底有自适应的避震鞋（学习率调整）👟

• 前期还会做“热身”（偏差校正）🔥
  → 一路平稳往谷底走，不会乱跳也不会卡住

和前面的优化器对比一下，得到如下的结果：

AdamW

权重衰减

在介绍AdamW之前，我们需要先理解一下权重衰减的概念。

权重衰减指的是在训练过程中，让模型参数自动变小，从而防止过拟合，需要权重衰减主要有两个原因：

1. 防止过拟合：参数太大可能在训练集上学得很好，但泛化能力差。衰减可以让它更“温和”地拟合数据。

2. 提升数值稳定性：过大的参数可能导致不稳定，比如梯度爆炸或输出范围奇怪（尤其在 softmax/logits 中）

一般而言，在训练模型时，对于Loss我们有：

比如交叉熵损失、均方误差之类的。

为了进行权重衰减，我们可以在计算Loss时加入一个L2正则项：

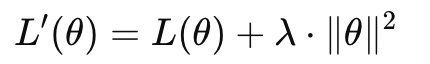
• L(θ)是原本的损失（衡量模型对训练集的拟合）

• ||θ||^2 是参数向量的平方和（越大说明参数越激进）

• λ是一个超参数，控制“惩罚力度”

对于SGD，在加入了L2正则项后，损失函数再对θ求导可以得到：

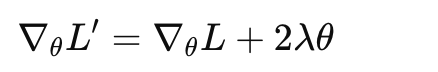
再把 2λ 合并写成 λ，并将参数写全就可以得到：

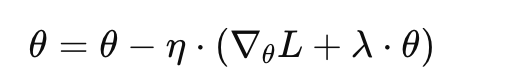
再整理一下得到：

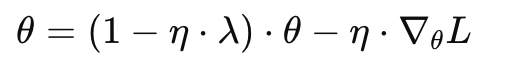
而在SGD加L2正则可以做到权重衰减，但是对于Adam却有了问题，因为Adam 中每个参数的更新方向会被“除以一个平方根的梯度平方平均”，也就是：

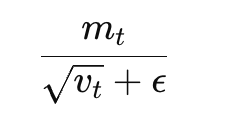
如果把 λ⋅θ加到这里就会导致梯度方向被缩放，权重衰减也被缩放！从而导致衰减效果不稳定，容易衰减不到位或者过头。

AdamW核心修改

为了解决Adam中权重衰减的问题，AdamW的做法是不把 λ⋅θ 当做“梯度的一部分”加进去，而是直接减掉，

AdamW下，参数更新的公式变成了：

θ = θ - η * ∇L - η * λ * θ

即直接减掉，不去受到学习率更新的影响。