深度学习中反向传播及优化器使用详解

反向传播

偏导数

参考资料：

简要说明：

  • 对于复合函数，如果要求其对于某一个参数的偏导数，那么就需要把其他参数看为常数，然后求导。

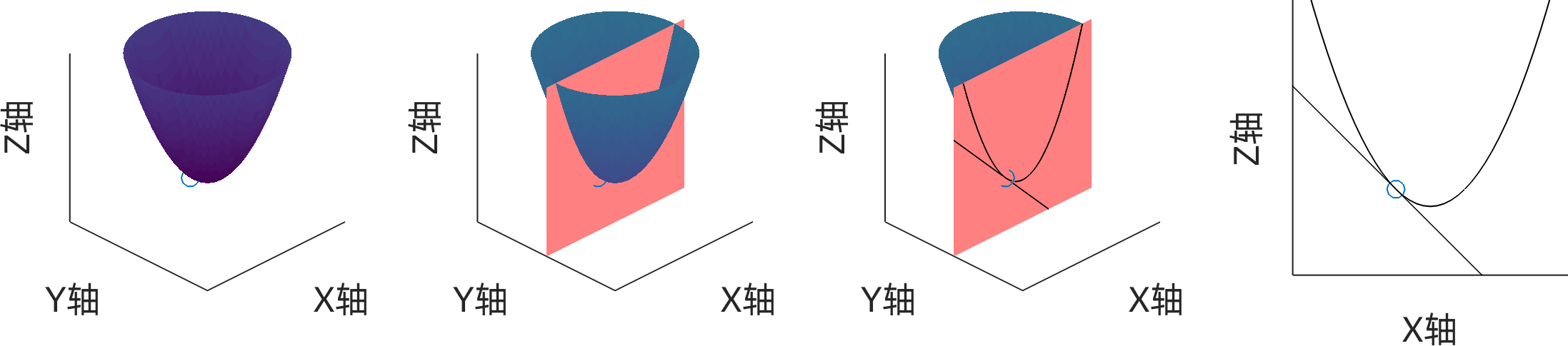
  • 几何意义：可以认为是沿着某一个轴的导数。如下图所示，对于曲面 $z=f(x,y)$对x的偏导就是求这个曲面上的某点对于x轴的斜率。

全微分

参考资料：

简要说明：

  • 对于多元函数，若每个参数都进行微小的变化，那么整个函数的z变化就是：$\mathrm{d}z=\sum_{i=1}^N\frac{\partial f}{\partial x_i}\mathrm{d}x_i$

  • 几何意义：对于曲面 $z=f(x,y)$，若它在 $(x_0, y_0)$附近的曲面光滑，那么考虑一个足够小的区域，可以把这附近近似为一个平面，若在$x$与$y$方向都都进行小幅的移动，则$z$的增量就等于先在$x$方向进行移动的增量再加上$y$方向移动的增量。

链式法则

参考资料：

简要说明：

  • 证明：

    • 假设现在有函数： $z(x,y)=f[u(x,y),v(x,y)]$

    • 根据全微分关系有： $\mathrm{d}z=\frac{\partial f}{\partial u}\operatorname{d}u+\frac{\partial f}{\partial v}\operatorname{d}v$

    • 对于 $du、dv$又有：$\mathrm{d}u=\frac{\partial u}{\partial x}\mathrm{d}x+\frac{\partial u}{\partial y}\mathrm{d}y, F\quad\mathrm{d}v=\frac{\partial v}{\partial x}\mathrm{d}x+\frac{\partial v}{\partial y}\mathrm{d}y$

    • 带入可得： $\begin{gathered}
      \mathbf{d}z=\frac{\partial f}{\partial u}{\left(\frac{\partial u}{\partial x}\right.}\mathrm{d}x+\frac{\partial u}{\partial y}\left.\mathrm{d}y\right)+\frac{\partial f}{\partial v}{\left(\frac{\partial v}{\partial x}\right.}\mathrm{d}x+\frac{\partial v}{\partial y}\left.\mathrm{d}y\right) \ =\left(\frac{\partial f}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial f}{\partial v}\frac{\partial v}{\partial x}\right)\mathrm{d}x+\left(\frac{\partial f}{\partial u}\frac{\partial u}{\partial y}+\frac{\partial f}{\partial v}\frac{\partial v}{\partial y}\right)\mathrm{d}y
      \end{gathered}$

    • 根据全微分的定义就可以得到： $\begin{aligned}
      \frac{\partial z}{\partial x} & =\frac{\partial f}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial f}{\partial v}\frac{\partial v}{\partial x}, \
      \
      \frac{\partial z}{\partial y} & =\frac{\partial f}{\partial u}\frac{\partial u}{\partial y}+\frac{\partial f}{\partial v}\frac{\partial v}{\partial y}\mathrm{~.}
      \end{aligned}$

    • 拓展到任意多变量的情况： $z(x_1,\ldots,x_N)=f[u_1(x_1,\ldots,x_N),\ldots,u_M(x_1,\ldots,x_N)]$

    • 我们就可以得到链式法则：$\Large\frac{\partial z}{\partial x_i}=\sum_j\frac{\partial f}{\partial u_j}\frac{\partial u_j}{\partial x_i}$

举例分析

假设现在有一个计算式为 $e=(a+b)(b+1)$，可以首先取 $c=a+b，d=b+1$，从而将其转化为 $e=cd$，然后根据链式法则可以求b的偏导： $\frac{\partial e}{\partial b}=\frac{\partial e}{\partial c}\frac{\partial c}{\partial b}+\frac{\partial e}{\partial d}\frac{\partial d}{\partial b}=d1+c1=(b+1)+(a+b)$。

取 $a=3, b=2$，将计算图绘制如下：

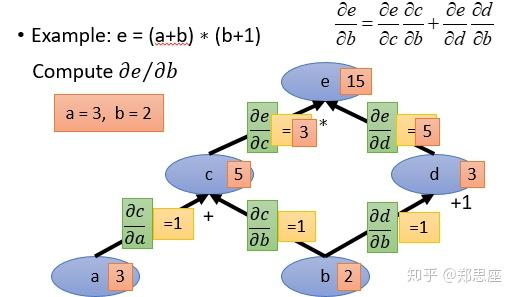
该图中是将数值作为了节点，将运算符作为了边。注意也有一些说法是反过来的。

在计算图中我们可以将各个变量的值计算出来，然后进行反向传播，计算去其对于各个变量的偏导数。对于 $b$，带入链式法则的公司，得到其偏导为 $\frac{\partial e}{\partial b}=\frac{\partial e}{\partial c}\frac{\partial c}{\partial b}+\frac{\partial e}{\partial d}\frac{\partial d}{\partial b}=31+51=8$。

带入计算图中可以更为简单地理解为其偏导就是各个链路的偏导乘积的和。所以如果我们需要同时计算 $a$和 $b$的偏导，我们可以将e节点认定为1，然后进行反向传播，求出各节点的偏导，然后进行复用，如下图所示：

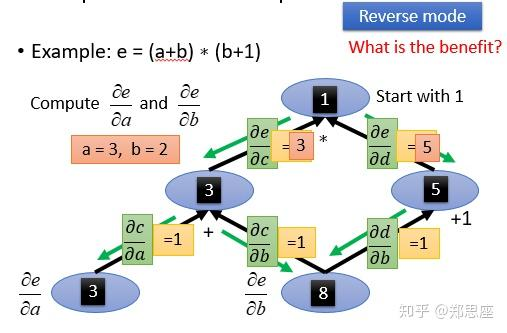
举例pytorch验证

使用pytorch实现上述的计算式，如下，最后的输出与我们上述分析的一致。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import torch

# 定义变量 a 和 b，并开启自动求导
a = torch.tensor(3.0, requires_grad=True)
b = torch.tensor(2.0, requires_grad=True)

# 构造计算式 e = (a + b)(b + 1)
c = a + b
d = b + 1
e = c * d  # e = (a + b) * (b + 1)

# 保留计算过程的梯度，默认pytorch只保留叶子节点的，所以需要主动设置
c.retain_grad()
d.retain_grad()
e.retain_grad()

# 反向传播求导
e.backward()

# 打印结果
print(f"e = {e.item()}")
print(f"∂e/∂e = {e.grad.item()}") 
print(f"∂e/∂c = {c.grad.item()}") 
print(f"∂e/∂d = {d.grad.item()}") 
print(f"∂e/∂a = {a.grad.item()}")  # 应该是 d = b + 1 = 3
print(f"∂e/∂b = {b.grad.item()}")  # 应该是 (∂e/∂c)*(∂c/∂b) + (∂e/∂d)*(∂d/∂b) = d + c = 3 + 5 = 8

# 输出
# e = 15.0
# ∂e/∂e = 1.0
# ∂e/∂c = 3.0
# ∂e/∂d = 5.0
# ∂e/∂a = 3.0
# ∂e/∂b = 8.0

优化器

上述我们知道了如何计算梯度，但是在实际的深度学习中，我们往往还需要构建模型，然后利用优化器对模型参数进行更新。

所以进一步，我们需要：

  1. 把 b 设为“模型参数”（可优化的变量）；

  2. 将 e = (a + b)(b + 1) 作为模型的“前向计算”；

  3. 定义损失函数（比如 loss = e ** 2，希望 e 趋近于 0）；

  4. 使用 optimizer 优化变量 b。

完整代码及输出如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
import torch
import torch.nn as nn
import torch.optim as optim

# 假设 a 是常数，b 是我们要学习的参数
a = torch.tensor(3.0)

# 将 b 作为参数需要被优化，requires_grad=True
b = torch.tensor(2.0, requires_grad=True)

# 构建优化器，优化目标是 b
optimizer = optim.SGD([b], lr=0.01)

# 训练目标：希望 e 趋近于 0，所以目标是最小化 loss = e^2
for epoch in range(20):
    optimizer.zero_grad()  # 清除旧梯度

    # 前向计算
    c = a + b
    d = b + 1
    e = c * d

    # 构造损失函数（比如希望 e 接近 0）
    loss = e ** 2  # 损失函数 L = e^2

    # 反向传播
    loss.backward()

    # 梯度更新
    optimizer.step()

    # 打印当前值
    print(f"Epoch {epoch+1:2d}: ∂loss/∂b = {b.grad.item():.4f}, b = {b.item():.4f}, e = {e.item():.4f}, loss = {loss.item():.4f}")

# Epoch  1: ∂loss/∂b = 240.0000, b = -0.4000, e = 15.0000, loss = 225.0000
# Epoch  2: ∂loss/∂b = 9.9840, b = -0.4998, e = 1.5600, loss = 2.4336
# Epoch  3: ∂loss/∂b = 7.5037, b = -0.5749, e = 1.2505, loss = 1.5637
# Epoch  4: ∂loss/∂b = 5.8771, b = -0.6336, e = 1.0310, loss = 1.0629
# Epoch  5: ∂loss/∂b = 4.7381, b = -0.6810, e = 0.8669, loss = 0.7515
# Epoch  6: ∂loss/∂b = 3.9025, b = -0.7201, e = 0.7397, loss = 0.5471
# Epoch  7: ∂loss/∂b = 3.2678, b = -0.7527, e = 0.6383, loss = 0.4074
# Epoch  8: ∂loss/∂b = 2.7723, b = -0.7805, e = 0.5557, loss = 0.3088
# Epoch  9: ∂loss/∂b = 2.3771, b = -0.8042, e = 0.4873, loss = 0.2375
# Epoch 10: ∂loss/∂b = 2.0561, b = -0.8248, e = 0.4299, loss = 0.1848
# Epoch 11: ∂loss/∂b = 1.7916, b = -0.8427, e = 0.3811, loss = 0.1453
# Epoch 12: ∂loss/∂b = 1.5709, b = -0.8584, e = 0.3393, loss = 0.1151
# Epoch 13: ∂loss/∂b = 1.3846, b = -0.8723, e = 0.3032, loss = 0.0919
# Epoch 14: ∂loss/∂b = 1.2261, b = -0.8845, e = 0.2718, loss = 0.0739
# Epoch 15: ∂loss/∂b = 1.0900, b = -0.8954, e = 0.2443, loss = 0.0597
# Epoch 16: ∂loss/∂b = 0.9725, b = -0.9051, e = 0.2201, loss = 0.0484
# Epoch 17: ∂loss/∂b = 0.8702, b = -0.9138, e = 0.1987, loss = 0.0395
# Epoch 18: ∂loss/∂b = 0.7809, b = -0.9217, e = 0.1797, loss = 0.0323
# Epoch 19: ∂loss/∂b = 0.7023, b = -0.9287, e = 0.1628, loss = 0.0265
# Epoch 20: ∂loss/∂b = 0.6331, b = -0.9350, e = 0.1477, loss = 0.0218

注意我们这里定义了 $loss=e^2$，所以在原计算图的最上面会多出一个节点，然后会多出一条边，这条边对应的偏导是 $\frac{\partial loss}{\partial e}=2e$。

对于Epoch 1，手动计算其相对于 $b$的导数为 $2e\frac{\partial e}{\partial b}=2158=240$。然后因为采取的是SGD且学习率为0.01，所以更新 $b = 2 - 0.01240= -0.4$。

而一般来说，我们会将其封装成模型进行使用，如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
import torch
import torch.nn as nn
import torch.optim as optim

class SimpleModel(nn.Module):
    def __init__(self, init_b):
        super().__init__()
        self.b = nn.Parameter(torch.tensor(init_b))

    def forward(self, a):
        c = a + self.b
        d = self.b + 1
        e = c * d
        return e

a = torch.tensor(3.0)
model = SimpleModel(init_b=2.0)
optimizer = optim.SGD(model.parameters(), lr=0.01)

for epoch in range(20):
    optimizer.zero_grad()
    e = model(a)
    loss = e ** 2
    loss.backward()
    optimizer.step()
    print(f"Epoch {epoch+1:2d}: ∂loss/∂b = {model.b.grad.item():.4f}, b = {model.b.item():.4f}, e = {e.item():.4f}, loss = {loss.item():.4f}")

# 输出结果：
# Epoch  1: ∂loss/∂b = 240.0000, b = -0.4000, e = 15.0000, loss = 225.0000
# Epoch  2: ∂loss/∂b = 9.9840, b = -0.4998, e = 1.5600, loss = 2.4336
# Epoch  3: ∂loss/∂b = 7.5037, b = -0.5749, e = 1.2505, loss = 1.5637
# Epoch  4: ∂loss/∂b = 5.8771, b = -0.6336, e = 1.0310, loss = 1.0629
# Epoch  5: ∂loss/∂b = 4.7381, b = -0.6810, e = 0.8669, loss = 0.7515
# Epoch  6: ∂loss/∂b = 3.9025, b = -0.7201, e = 0.7397, loss = 0.5471
# Epoch  7: ∂loss/∂b = 3.2678, b = -0.7527, e = 0.6383, loss = 0.4074
# Epoch  8: ∂loss/∂b = 2.7723, b = -0.7805, e = 0.5557, loss = 0.3088
# Epoch  9: ∂loss/∂b = 2.3771, b = -0.8042, e = 0.4873, loss = 0.2375
# Epoch 10: ∂loss/∂b = 2.0561, b = -0.8248, e = 0.4299, loss = 0.1848
# Epoch 11: ∂loss/∂b = 1.7916, b = -0.8427, e = 0.3811, loss = 0.1453
# Epoch 12: ∂loss/∂b = 1.5709, b = -0.8584, e = 0.3393, loss = 0.1151
# Epoch 13: ∂loss/∂b = 1.3846, b = -0.8723, e = 0.3032, loss = 0.0919
# Epoch 14: ∂loss/∂b = 1.2261, b = -0.8845, e = 0.2718, loss = 0.0739
# Epoch 15: ∂loss/∂b = 1.0900, b = -0.8954, e = 0.2443, loss = 0.0597
# Epoch 16: ∂loss/∂b = 0.9725, b = -0.9051, e = 0.2201, loss = 0.0484
# Epoch 17: ∂loss/∂b = 0.8702, b = -0.9138, e = 0.1987, loss = 0.0395
# Epoch 18: ∂loss/∂b = 0.7809, b = -0.9217, e = 0.1797, loss = 0.0323
# Epoch 19: ∂loss/∂b = 0.7023, b = -0.9287, e = 0.1628, loss = 0.0265
# Epoch 20: ∂loss/∂b = 0.6331, b = -0.9350, e = 0.1477, loss = 0.0218

参考资料

  1. https://blog.csdn.net/weixin\_43314579/article/details/88937475

  2. https://zhuanlan.zhihu.com/p/85147199

  3. https://wuli.wiki/online/PChain.html

  4. https://zh.wikipedia.org/wiki/%E9%93%BE%E5%BC%8F%E6%B3%95%E5%88%99

  5. https://zhuanlan.zhihu.com/p/111402123

LLM
#AI #pytorch
深度学习中反向传播及优化器使用详解
http://example.com/2025/06/07/pytorchBackPropagation/
作者
滑滑蛋
发布于
2025年6月7日
许可协议