基础强化学习学习笔记
基础概念
环境:系统提供的基础环境
状态:环境会被Agent的动作改变,从而变为不同的状态
奖励:环境需要根据当前状态与Agent的动作产生一个奖励来衡量当前动作的好坏
Agent:依据当前环境进行决策,执行相关动作的对象
动作:Agent实际执行的动作,改变环境到下一个状态
决策:依据当前环境可能会产生多个动作,每个动作有不同的概率
动作状态转移概率:执行一个动作可能会转移到不同的状态,一个动作的状态转移存在一个概率分布
马尔可夫:
- 马尔可夫性质:某时刻的状态只取决于上一时刻的状态时
即当前的状态反映了过去所有状态的累积结果,决策只需要看当前的状态,而不再需要考虑过去几次的状态。例如下象棋,只需要关注当前的棋局。而一个不怎么严谨的反例就是看股票走势,这不能只看当前的股票价格也要关注过去一段其走势。
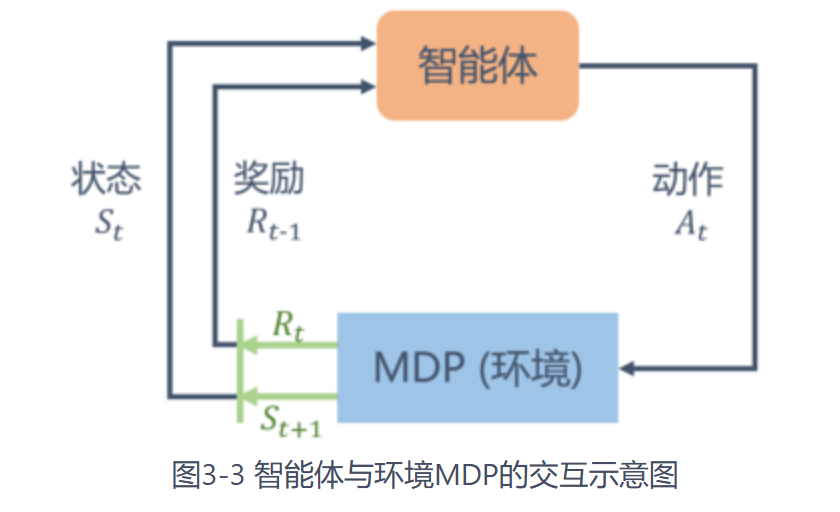
马尔可夫决策过程(Markov decision process,MDP):
其由元组<S, A, P, r, γ>构成,其中:
S是状态的集合;
A是动作的集合;
γ是折扣因子;
r(s, a) 是奖励函数,此时奖励可以同时取决于状态s和动作a,在奖励函数只取决于状态s时,则退化为r(s);
P(s’|s, a) 是状态转移函数,表示在状态s执行动作a之后到达状态s’的概率。
策略(Policy):通常用字母π表示。策略π是一个函数 $π(a|s)=P(A_t = a|S_t = s) $,表示在输入状态s情况下采取动作a的概率
回报(Return):在一个马尔可夫决策过程中从某一个状态 $S_t$开始直到终止状态的所有奖励的衰减之和,即$G_t=R_t+\gamma R_{t+1}+\gamma^2R_{t+2}+\cdots=\sum_{k=0}^\infty\gamma^kR_{t+k}$
动作价值函数(State-Value Function):从状态s出发遵循策略π能获得的期望回报,即 $V^\pi(s)=\mathbb{E}_\pi[G_t|S_t=s]$
状态价值函数(Action-Value Function):在状态s下采取动作a之后遵循策略π能获得的期望回报,即 $Q^\pi(s,a)=\mathbb{E}_\pi[G_t|S_t=s,A_t=a]$
贝尔曼期望方程(Bellman Expectation Equation):将其上述动作、状态价值函数均往后再看一步,推导到自举的形式,即:
$$V^{\pi}(s)=\mathbb{E}_\pi[R_t+\gamma V^\pi(S_{t+1})|S_t=s] =\sum_{a\in A}\pi(a|s)\left(r(s,a)+\gamma\sum_{s^{\prime}\in S}p(s^{\prime}|s,a)V^\pi(s^{\prime})\right)$$
$$\begin{aligned}
Q^\pi(s,a) & =\mathbb{E}_\pi[R_t+\gamma Q^\pi(S_{t+1},A_{t+1})|S_t=s,A_t=a] =r(s,a)+\gamma\sum_{s^{\prime}\in S}p(s^{\prime}|s,a)\sum_{a^{\prime}\in A}\pi(a^{\prime}|s^{\prime})Q^\pi(s^{\prime},a^{\prime})
\end{aligned}$$最终目标:找到一个策略使得在各状态下执行获得的期望价值最高,解决手段分为两类,Value-base方法和Policy-base方法
Value-base方法
Value-base方法的主要目标是求得价值函数,其不需要显性的更新策略,其策略默认为每次选取价值最高的动作来执行。
其方法可划分为:
蒙特卡罗方法
时序差分
SARSA
Q-learning->DQN
蒙特卡罗方法
其首先会使用策略π采样出大量完整的序列
最简单的方法是统计各序列中出现的各状态的次数以及状态对应的回报之和,然后以此计算出回报的平均值,将其作为各状态的价值估计
也可以采用增量式更新的方法,对于每个状态s和对应回报G进行如下计算
$$N(s)\leftarrow N(s)+1$$
$$V(s)\leftarrow V(s)+\frac{1}{N(s)}(G-V(S))$$
上述是计算价值函数的方法,对于计算动作价值函数也是类似的方法
蒙特卡罗方法的特点是其其是无偏的,但是方差较大
这里V(s)的计算是一个秋平均值计算时的小技巧,推导如下:
已经有了前N(s)-1次的价值估值: $$V_{N(s)-1}(s)=\frac{1}{N(s)-1}\sum_{i=1}^{N(s)-1}G_i$$
加入第N(s)次的回报后可以推导为:
$$\begin{aligned}
V_{N(s)}(s) & =\frac{1}{N(s)}\left(\sum_{i=1}^{N(s)-1}G_i+G\right) \
& =\frac{1}{N(s)}\left((N(s)-1)V_{N(s)-1}(s)+G\right) \
& =V_{N(s)-1}(s)+\frac{1}{N(s)}\left(G-V_{N(s)-1}(s)\right)
\end{aligned}$$
- 而这也就是上述V(s)的更新公式
时序差分
蒙特卡罗的一个问题在于每次更新状态价值时都需要计算该状态在序列往后所有的回报,其更新频率很低
而时序差分方法只需要当前步结束即可进行计算,它使用当前获得的奖励加上下一个状态的价值来估计该状态获得的回报,即 $G =r_t+\gamma V(s_{t+1})$,然后再使用与蒙特卡罗中增量更新方法类似的计算方式进行更新,不过将 $\frac{1}{N(s)}$替换为了 $\alpha$,从而得到如下的更新公式:
$$V(s_t)\leftarrow V(s_t)+\alpha[r_t+\gamma V(s_{t+1})-V(s_t)]$$
其中 $r_t+\gamma V(s_{t+1})-V(s_t)$通常被称为时序差分(temporal difference,TD)误差(error)
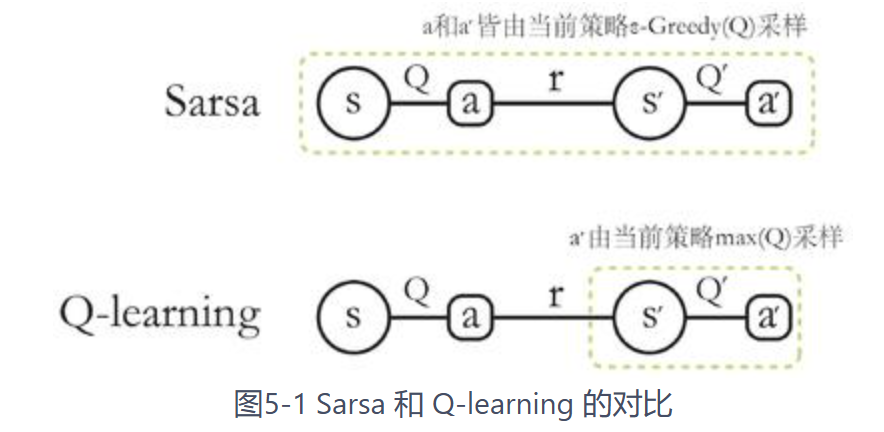
SARSA
- 而要做策略迭代,我们更需要关注的是动作价值,同样的采用时序差分方法,我们可以对动作价值使用类似的如下的更新方式:$Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\alpha[r_t+\gamma Q(s_{t+1},a_{t+1})-Q(s_t,a_t)]$
注意其在采样时并不是每次都是执行价值最高的动作,因为那会使得采样的多样性不足,其往往采用 $\epsilon$-贪婪策略,即以 $\epsilon$的概率随机选择,再以$1-\epsilon$的概率选择价值最高的动作
- 进一步的还有多步SARSA算法,其在估计回报的时候使用多次奖励,其更新方式为: $$Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\alpha[r_t+\gamma r_{t+1}+\cdots+\gamma^nQ(s_{t+n},a_{t+n})-Q(s_t,a_t)]$$
Q-learning
Q-learning算法也是采取时序差分的更新方式,不同点在于在估计回报时它不是采用了当前序列中下一个状态会采取的动作,而是选取了获得价值最高的动作,最终使得其更新方式变为了: $$Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\alpha[R_t+\gamma\max_aQ(s_{t+1},a)-Q(s_t,a_t)]$$
其一大特点是其在更新的时候使用的并不是当前策略,所以也被称为离线策略,而SARSA策略使用的一直是当前策略,所以被称为在线策略
DQN
Q-learning需要以矩阵的方式存储不同状态下各动作的Q值,但是在复杂场景中由于状态与动作过大,难以用表格逐个记录,所以引申出了使用深度学习模型来拟合Q值的方法
为了使得模型拟合Q值更加精准,参考Q-learning的更新方式,我们可以将loss定义为均方误差的形式,如下所示:
$$L=\frac{1}{N}\sum_{i=1}^N\left[Q_\omega\left(s_i,a_i\right)-\left(r_i+\gamma\max_{a^{\prime}}Q_\omega\left(s_i^{\prime},a^{\prime}\right)\right)\right]^2$$
为了使得DQN训练更稳定,往往还会采取如下的设计:
经验回放:维护一个回放缓冲区,将每次从环境中采样得到的四元组数据(状态、动作、奖励、下一状态)存储到回放缓冲区中,训练 Q 网络的时候再从回放缓冲区中随机采样若干数据来进行训练。这可以打破样本之间的相关性,让其满足独立假设。并且提高了样本效率,使得每一个样本可以被使用多次
目标网络:DQN 算法最终更新的目标是让 $Q_\omega\left(s,a\right)$逼近 $r+\gamma\max_{a^{\prime}}Q_{\omega}\left(s^{\prime},a^{\prime}\right)$,由于 TD 误差目标本身就包含神经网络的输出,因此在更新网络参数的同时目标也在不断地改变,这非常容易造成神经网络训练的不稳定性。故其做法是使用两个网络,对于 $r_i+\gamma\max_aQ_{\omega^-}(s_{i+1},a)$中的 $Q_{\omega^-}$其在一个batch的训练中不会改变,一个batch训练结束后再与训练的 $Q_\omega\left(s,a\right)$进行同步
Policy-base方法
Policy-base方法中存在显式的策略,其的主要目标是不断更新策略函数获得更高的价值
其方法可划分为:
Policy Gradient系列:
REINFORCE
Actor-Critic
TRPO系列:
- TRPO->PPO
Policy Gradient系列
- 我们使用深度学习模型来模拟一个策略,其目标是要寻找一个最优策略并最大化这个策略在环境中的期望回报。我们将策略学习的目标函数定义为:
$$J(\theta)=\mathbb{E}_{s_0}[V^{\pi_\theta}(s_0)]$$, $s_0$表示初始状态
- 然后对目标函数求导,经过一系列计算可以得到导数:
$$\begin{aligned}
\nabla_\theta J(\theta) & \propto\sum_{s\in S}\nu^{\pi_\theta}(s)\sum_{a\in A}Q^{\pi_\theta}(s,a)\nabla_\theta\pi_\theta(a|s) \
& =\sum_{s\in S}\nu^{\pi_\theta}(s)\sum_{a\in A}\pi_\theta(a|s)Q^{\pi_\theta}(s,a)\frac{\nabla_\theta\pi_\theta(a|s)}{\pi_\theta(a|s)} \
& =\mathbb{E}_{\pi_\theta}[Q^{\pi_\theta}(s,a)\nabla_\theta\log\pi_\theta(a|s)]
\end{aligned}$$
直观理解一下策略梯度这个公式,可以发现在每一个状态下,梯度的修改是让策略更多地去采样到带来较高Q值的动作,更少地去采样到带来较低Q值的动作
注意这里的核心也是如何估计Q
REINFORCE
- REINFORCE 算法是采用了蒙特卡罗的方法来估计Q,即将一个序列中后续的奖励进行累积来当做Q,故而可以将梯度写成如下的样式:
$$\nabla_\theta J(\theta)=\mathbb{E}_{\pi_\theta}\left[\sum_{t=0}^T\left(\sum_{t^{\prime}=t}^T\gamma^{t^{\prime}-t}r_{t^{\prime}}\right)\nabla_\theta\log\pi_\theta(a_t|s_t)\right]$$
- 得到了梯度后就可以用梯度下降的方式来更新模型
Actor-Critic
Actor-Critic算法采用的方法是用模型来估计Q值:
可以使用DQN类似的,直接用模型来拟合Q值
也可以使用模型来拟合价值函数V,然后使用过时序差分残差 $r_t+\gamma V^{\pi_\theta}(s_{t+1})-V^{\pi_\theta}(s_t)$来替代 $Q^{\pi_\theta}(s,a)$来得到 $\nabla_\theta J(\theta)$,而对于价值函数模型的更新与前面DQN类似,可以将Loss定义为 $\mathcal{L}(\omega)=\frac{1}{2}(r+\gamma V_\omega(s_{t+1})-V_\omega(s_t))^2$来更新模型
TRPO系列
- 上述Policy Gradient的方法虽然简单、直观,但在实际应用过程中会遇到训练不稳定的情况,这是因为每一次沿着梯度进行参数更新的步长不好控制。在Actor-Critic算法的基础上TRPO方法提出了信任区域(trust region),使得在这个区域内进行参数更新肯定能使得效果大于等于原策略,并以此为基础衍生出了PPO算法。
TRPO
- 考虑到 $s_0$的分布与初始环境有关而与策略无关,所以旧策略的优化目标 $J(\theta)$可以用策略进行如下的推导:
$$\begin{aligned}
J(\theta) & =\mathbb{E}_{s_0}[V^{\pi_\theta}(s_0)] \
& =\mathbb{E}_{\pi_{\theta^{\prime}}}\left[\sum_{t=0}^\infty\gamma^tV^{\pi_\theta}(s_t)-\sum_{t=1}^\infty\gamma^tV^{\pi_\theta}(s_t)\right] \
& =-\mathbb{E}_{\pi_{\theta^{\prime}}}\left[\sum_{t=0}^\infty\gamma^t\left(\gamma V^{\pi_\theta}(s_{t+1})-V^{\pi_\theta}(s_t)\right)\right]
\end{aligned}$$
- 以此为基础,新旧策略的目标函数之间的差距可以计算如下:
$$\begin{aligned}
J(\theta^{\prime})-J(\theta) & =\mathbb{E}_{s_0}\left[V^{\pi_{\theta^{\prime}}}(s_0)\right]-\mathbb{E}_{s_0}\left[V^{\pi_\theta}(s_0)\right] \
& =\mathbb{E}_{\pi_{\theta^{\prime}}}\left[\sum_{t=0}^\infty\gamma^tr(s_t,a_t)\right]+\mathbb{E}_{\pi_{\theta^{\prime}}}\left[\sum_{t=0}^\infty\gamma^t\left(\gamma V^{\pi_\theta}(s_{t+1})-V^{\pi_\theta}(s_t)\right)\right] \
& =\mathbb{E}_{\pi_{\theta^{\prime}}}\left[\sum_{t=0}^\infty\gamma^t\left[r(s_t,a_t)+\gamma V^{\pi_\theta}(s_{t+1})-V^{\pi_\theta}(s_t)\right]\right]
\end{aligned}$$
里面的$r(s_t,a_t)+\gamma V^{\pi_\theta}(s_{t+1})-V^{\pi_\theta}(s_t)$就是时序差分残差,将其定义为A,得到
$J(\theta^{\prime})-J(\theta)=\mathbb{E}_{\pi_{\theta^{\prime}}}\left[\sum_{t=0}^\infty\gamma^tA^{\pi_\theta}(s_t,a_t)\right]$
为了进行策略迭代,我们需要找到一个新策略 $\pi_{\theta^{\prime}}$,使得 $\mathbb{E}_{\pi_{\theta^{\prime}}}\left[\sum_{t=0}^\infty\gamma^tA^{\pi_\theta}(s_t,a_t)\right]$大于0,而这存在的问题在于该公式中是对新策略 $\pi_{\theta^{\prime}}$求的期望,而此时我们还没有新策略,故方法是进行一定程度的近似。
首先将 $J(\theta^{\prime})-J(\theta)$进一步展开可以得到:$$J(\theta^{\prime})-J(\theta)=\mathbb{E}_{\pi_{\theta^{\prime}}}\left[\sum_{t=0}^\infty\gamma^tA^{\pi_\theta}(s_t,a_t)\right]=\mathbb{E}_{s_t\sim P_t^{\pi_{\theta^{\prime}}}}\left[\mathbb{E}_{a_t\sim\pi_{\theta^{\prime}}(\cdot|s_t)}\left[\gamma^tA^{\pi_\theta}(s_t,a_t)\right]\right]$$
然后我们假设两个策略的差别较小,所以两者的状态访问分布P基本相同,所以直接采用原策略的P,得到如下:$$J(\theta^{\prime})-J(\theta)=\mathbb{E}_{s_t\sim P_t^{\pi_{\theta}}}\left[\mathbb{E}_{a_t\sim\pi_{\theta^{\prime}}(\cdot|s_t)}\left[\gamma^tA^{\pi_\theta}(s_t,a_t)\right]\right]$$
然后借助重要性采样原理,我们可以原策略的基础上通过添加概率比值来替换新策略的动作概率分布,进一步可以得到:$$J(\theta^{\prime})-J(\theta)=\mathbb{E}_{s_t\sim P_t^{\pi_{\theta}}}\left[\mathbb{E}_{a_t\sim\pi_{\theta}(\cdot|s_t)}\left[\frac{\pi_{\theta^{\prime}}(a|s)}{\pi_\theta(a|s)}\gamma^tA^{\pi_\theta}(s_t,a_t)\right]\right]$$
- 重要性采样可以这么简单理解,现在存在一个新函数p(x),还有一个旧函数q(x),因为f(x)不变,两者只有概率不同,所以求新函数的期望时可以转变为: $$\begin{aligned}
& \mathbb{E}_{x\sim p(x)}[f(x)] \
& =\int_xq(x)\frac{p(x)}{q(x)}f(x)dx=\mathbf{E}_{x\sim q(x)}\left[\frac{p(x)}{q(x)}f(x)\right]
\end{aligned}$$
- 重要性采样可以这么简单理解,现在存在一个新函数p(x),还有一个旧函数q(x),因为f(x)不变,两者只有概率不同,所以求新函数的期望时可以转变为: $$\begin{aligned}
可以将 $\gamma$去掉,最终得到了整体的优化公式:
$$\begin{aligned} argmax_{\theta^{\prime}} \mathbb{E}_{s\sim \nu_{\theta},a\sim \pi_\theta(\cdot|s)}\left[\frac{\pi_{\theta^{\prime}}(a|s)}{\pi_\theta(a|s)}A^{\pi_\theta}(s,a)\right] \mathrm{s.t.}\mathbb{E}_{s\sim\nu^{\pi_{\theta_{k}}}}[D_{KL}(\pi_{\theta_{k}}(\cdot|s),\pi_{\theta^{\prime}}(\cdot|s))]\leq\delta
\end{aligned}$$
其中下面的不等式约束定义了策略空间中的一个 KL 球,被称为信任区域。在这个区域中,可以认为当前学习策略和环境交互的状态分布与上一轮策略最后采样的状态分布一致,进而可以基于一步行动的重要性采样方法使当前学习策略稳定提升。
一般是使用 KL 散度的 二阶泰勒展开 来构造信赖域: $\mathbb{E}[D_{\mathrm{KL}}(\pi_{\mathrm{old}}|\pi_\theta)]\approx\frac{1}{2}(\theta-\theta_{\mathrm{old}})^TH(\theta-\theta_{\mathrm{old}})$,其中H表示策略之间平均 KL 距离的黑塞矩阵(Hessian matrix)。
TRPO最终作为一个最优化方法,其可以使用近似求解、共轭梯度、线性搜索、广义优势估计等方法,具体见https://hrl.boyuai.com/chapter/2/trpo%E7%AE%97%E6%B3%95
PPO
TRPO的问题在于其计算量过大,为了解决该问题,PPO算法被提出。PPO 有两种形式,一是 PPO-惩罚,二是 PPO-截断。
PPO-惩罚用拉格朗日乘数法直接将 KL 散度的限制放进了目标函数中,这就变成了一个无约束的优化问题,在迭代的过程中不断更新 KL 散度前的系数。即:
$$\begin{aligned}
& argmax_{\theta^{\prime}} \mathbb{E}_{s\sim \nu_{\theta},a\sim \pi_\theta(\cdot|s)}\left[\frac{\pi_{\theta^{\prime}}(a|s)}{\pi_\theta(a|s)}A^{\pi_\theta}(s,a)-\beta D_{KL}(\pi_{\theta_{k}}(\cdot|s),\pi_{\theta^{\prime}}(\cdot|s))\right] \
\end{aligned}$$令 $d_k=D_{KL}^{\nu^{\pi_{\theta_k}}}(\pi_{\theta_k},\pi_\theta)$, $\beta$的更新规则如下
如果 $d_k<\delta/1.5$,那么 $\beta_k+1=\beta_k/2$
如果 $d_k>\delta\times1.5$,那么$\beta_k+1=\beta_k\times2$
否则$\beta_k+1=\beta_k$
其中, $\delta$是事先设定的一个超参数,用于限制学习策略和之前一轮策略的差距。
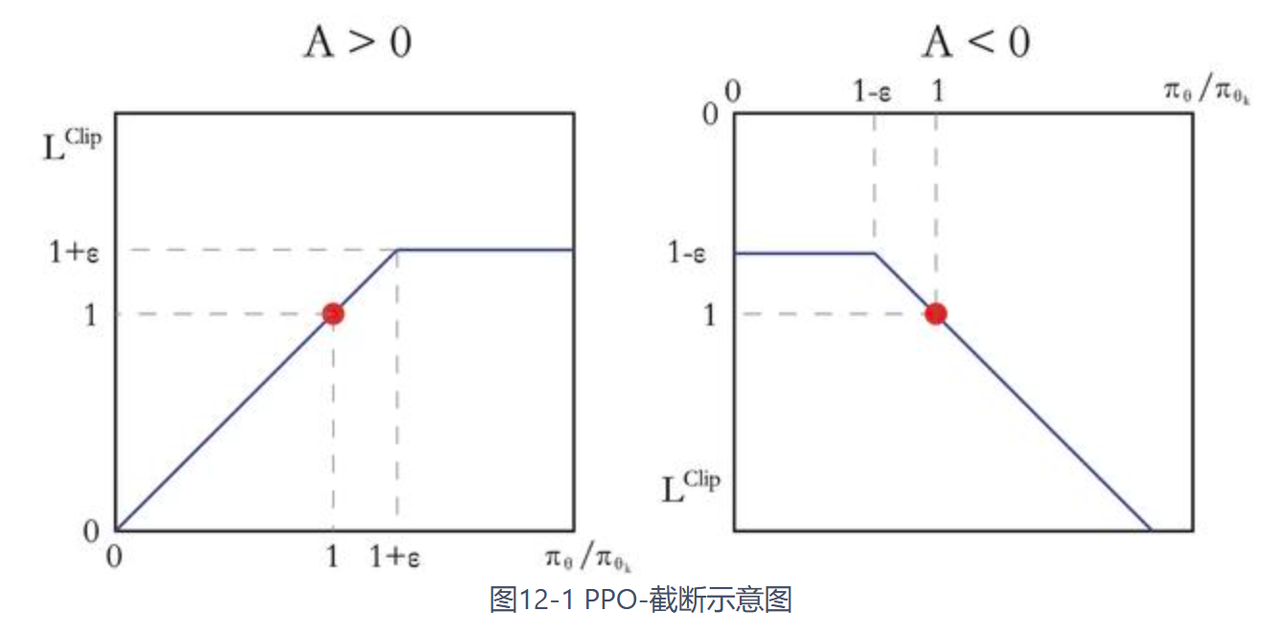
PPO-截断更加直接,它在目标函数中进行限制,以保证新的参数和旧的参数的差距不会太大,即:
$$argmax_{\theta^{\prime}} \mathbb{E}_{s\sim \nu_{\theta},a\sim \pi_\theta(\cdot|s)}\left[\min\left(\frac{\pi_{\theta^{\prime}}(a|s)}{\pi_\theta(a|s)}A^{\pi_{\theta}}(s,a),\mathrm{clip}\left(\frac{\pi_{\theta^{\prime}}(a|s)}{\pi_\theta(a|s)},1-\epsilon,1+\epsilon\right)A^{\pi_{\theta}}(s,a)\right)\right]$$
其中 $\operatorname{clip}(x,l,r)=\max(\min(x,r),l)$,将x限制在了l~r中间,然后再加上外面的min函数,对于A>0也就是好动作的情况,其将 $\frac{\pi_{\theta^{\prime}}(a|s)}{\pi_\theta(a|s)}$限制为了最大为 $1+\epsilon$,也就是好动作的概率最多只能增加到 $1+\epsilon$,对于A<0也就是坏动作的情况,其将 $\frac{\pi_{\theta^{\prime}}(a|s)}{\pi_\theta(a|s)}$限制为了最小为 $1-\epsilon$,也就是坏动作的概率最多只能减少到 $1-\epsilon$,如下所示。其效果就是不让概率剧烈的变化
需要注意的是,TRPO 和 PPO 都属于在线策略学习算法,即使优化目标中包含重要性采样的过程,但其只是用到了上一轮策略的数据,而不是过去所有策略的数据。
- 此外在实际训练PPO时往往采用的是 $A_t^{GAE}$,其与多步SARSA的思想类似,推导公式如下

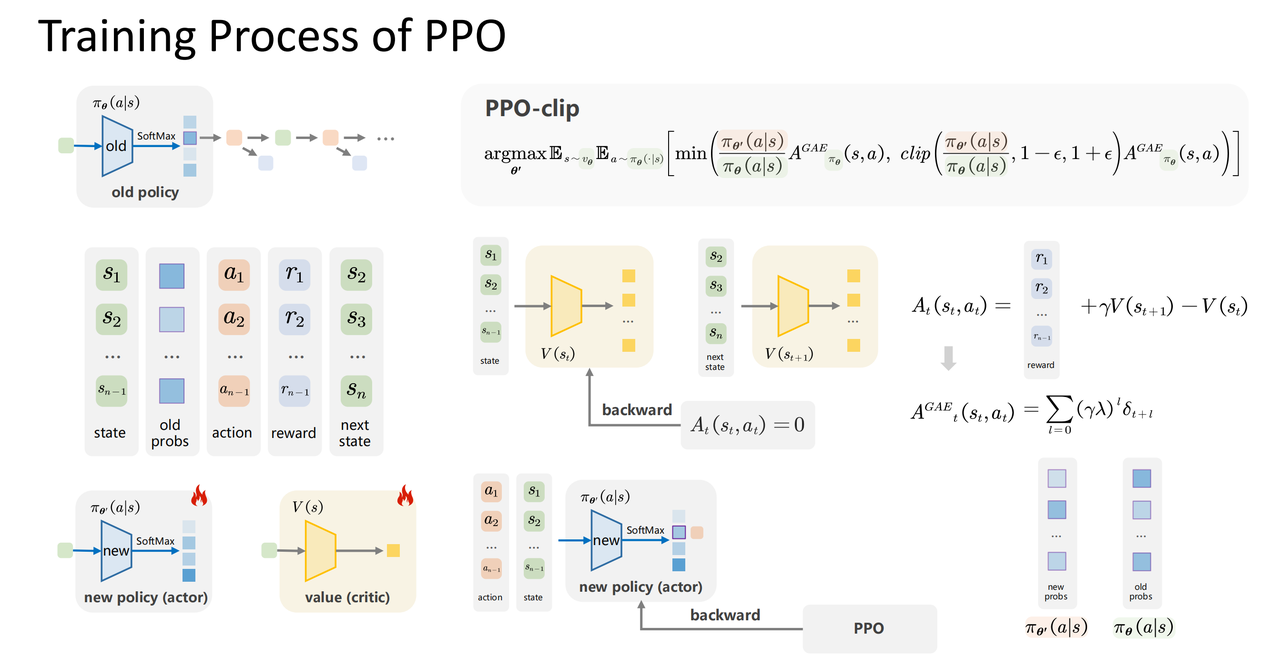
整体训练流程如下图所示:
初始化策略模型,价值模型
使用旧的策略模型生成一条序列
通过序列中的奖励r以及价值模型v得到 $A_t$,并进一步得到 $A_t^{GAE}$
计算新策略模型在这个状态s下采取a行动的策略好计算重要性采样中的权重
更新价值模型,价值模型的目标是使得时序差分残差A为0
使用PPO-clip更新策略模型